leetcode Wildcard Matching 题解 动态规划

发表于 | 分类于 |

原题

1
2
3
4
5
6
7
8
9
10
Given an input string (s) and a pattern (p), implement wildcard pattern matching with support for '?' and '*'.

'?' Matches any single character.
'*' Matches any sequence of characters (including the empty sequence).
The matching should cover the entire input string (not partial).

Note:

s could be empty and contains only lowercase letters a-z.
p could be empty and contains only lowercase letters a-z, and characters like ? or *.

题意比较简单，就是 ? 表示任何单个字符，* 表示0到多个字符。类似于正则表达式

那么就可以看出来，

  • 如果 s[i] == p[j] ，那就看 s[i+1…n], p[j+1…m] 是否匹配

  • 如果 s[i] != p[j] && p[j] == ‘?’ 同上

  • 如果 s[i] != p[j] && p[j] == ‘*’ 这种比较复杂

    • 如果 * 表示空字符 则是否匹配取决于 s[i…n], p[j+1…m]是否匹配
    • 如果 * 表示和s[i]相等的字符，则是否匹配取决于 s[i+1…n], p[j+1…m] 是否匹配
    • 如果* 表示继续匹配s字符串之后的字符，则是否匹配取决于 s[i+1…n], p[j…m]

  • 如果 s[i] != p[j] && p[j] != ‘?’ && p[j] != ‘*’ 则不匹配

通过以上的关系，就可以很轻松写出来递归，回溯的代码，但是这样是过不了的，当p中有很多*字符，那么肯定是超时的，效率很低

效率低是因为其中回溯的做法，没有记住中间状态，导致回溯过程中重复大量比较，浪费了时间。

如果用一个二维数组记住中间状态，就可以空间换时间，节约较多时间。

上面的四种情况，等价于 一下的等式

  • if s[i] == p[j] then dp[i][j] = dp[i+1][j+1]

  • if s[i] != p[j] && p[j] == ‘?’ then 同上

  • if s[i] != p[j] && p[j] == ‘*’ then dp[i][j] = dp[i+1][j+1] || dp[i+1][j] || dp[i][j+1]

  • if s[i] != p[j] && p[j] != ‘?’ && p[j] != ‘*’ then dp[i][j] = false

那么从等式就可以看出来前一个结果和回一个结果之间的依赖关系。

用题中给的例子，来画个图，

初始化

初始化的过程比较简单，其中需要注意的是3G的位置，由于匹配的是*，因此这个位置依赖于4G的位置

之后根据初始化的值和之前的依赖等式，就可以推导出来其他位置的值

第一轮

其中红色箭头就是依赖关系，还是比较清晰的，之后依次持续推算

结果

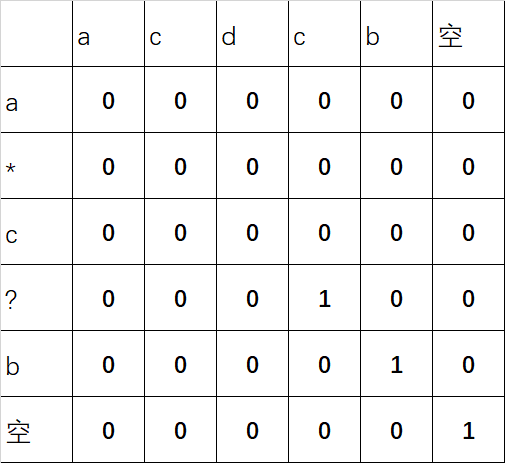
从最后图中可以看出dp[0][0] = false，所以不匹配，动态规划的做法记录了每一次计算的中间状态，省去了可能的大量重复计算，速度比较快。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

class Solution {

    public boolean isMatch(String s, String p) {
      if (p.equals("")) {
        return s.equals("");
      }
      
      return match(s.toCharArray(), s.length(), p.toCharArray(), p.length());
    }
    
    public boolean match(char[] s, int i, char[] p, int j) {
      boolean[][] dp = new boolean[i+1][j+1];
      dp[i][j] = true;
      for (int jj = j-1; jj>=0; --jj) {
        if (p[jj] == '*') {
          dp[i][jj] = dp[i][jj+1];
        }
      }
      
      for (int k=i-1; k>=0; --k) { // i
        for (int t=j-1; t>=0; --t) { // j
          if (s[k]== p[t] || p[t] == '?') {
            dp[k][t] = dp[k+1][t+1];
          } else {
            if (p[t] == '*') {
              dp[k][t] = dp[k+1][t+1] || dp[k][t+1] || dp[k+1][t];
            } else {
              dp[k][t] = false;
            }
          }
        }
      }
      
      return dp[0][0];
    }
}